Convective Heat Transfer Made (Very) Simple
As in the case of mass transport, the combination of simple plug flow with diffusion perpendicular to the streamlines allows simple first approximations for simple situations. Let's consider a simple example. We approximate the flow velocity as constant everywhere and assume that heat is carried by convection in the direction of gas flow and by conduction in the gas (obeying a 1-dimensional diffusion equation with time being the time in the stream) in the perpendicular direction.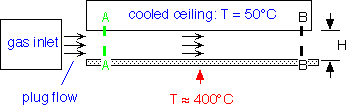
Near the entry region a narrow boundary layer exists near the hot wall, with the remainder of the gas at the initial temperature.
In the downstream region the temperature profile is essentially linear, as for a stationary conductive medium.
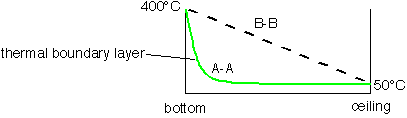
Since the heat loss is proportional to the gradient close to the surface, cooling is much larger in regions like A-A, where large gradients exist in the boundary layer.
As the gas heats up, thermal expansion must occur according to the ideal gas law. Thus, the velocity actually should increase as we go downstream. However, thermal diffusivity also increases, since the thermal conductivity increases as about T1.5, and the density decreases. The two effects tend to compensate (for small amounts of heating, anyway), so it's often convenient to ignore them to first order.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
