Convection: Fluid Flow and the Reynolds Number


Fluid Flow Made Simple: Ignore (Almost) Everything



Mass transport can occur due to motion of the bulk fluid or gas, whether or not concentration gradients exist. Anyone who has ever watched a smoker exhale or a leaf fall in a breeze knows this can be a very complex field! However, in many cases of interest for chemical vapor deposition flows are fairly simple (necessarily, as otherwise the machines could never be made to work!). How do we tell what sort of flow we're dealing with?
  • The first clue is the Reynolds number:
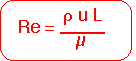
conv_1 conv_2

When Re is small (less than about 10), flows are typically very smooth: the "streamlines" (paths of imaginary test particles in the fluid) lie in neighboring layers or laminae, giving rise to the description of this "laminar" flow.

Laminar_flow

As Re grows large (hundreds to a few thousand) flows become more complex: first recirculations and vortices appear (in which the local velocity is opposed to the global average) ...
Recirc_flow

At high values of Re (thousands to millions) flow is complex and unpredictable in detail: turbulent.
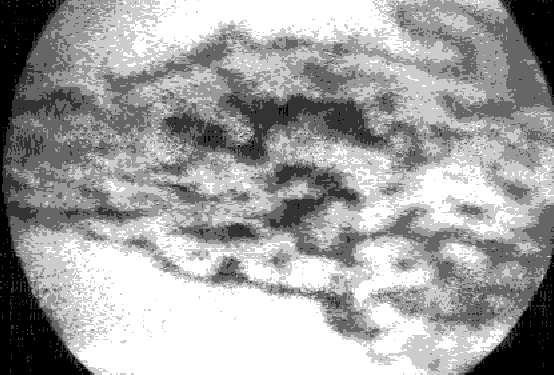
Turbulent_flow
Images: Flow Visualization (2nd ed.), W. Merzkirch, Academic Press 1987

  • Digression: What is Re?

To figure out the physical significance of this obscure combination of parameters, it is first useful to introduce the kinematic viscosity: the viscosity divided by the density:

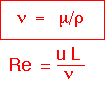
conv_5

Note that the kinematic viscosity has the dimensions of a diffusion coefficient:
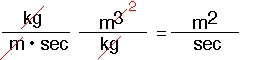
conv_6

It is interesting to note that it is also numerically of the same order as binary diffusion coefficients for gases: i.e. around 0.1 to 1 cm2/sec.

If we treat it as a diffusion coefficient, then we can calculate a diffusion length, using the residence time L/U:

conv_7

We then find that the Reynolds number is the square of the ratio of the system size to the diffusion length for momentum: Re is the Peclet number for momentum.

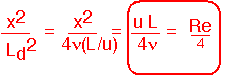
conv_8

We can now see that small Re corresponds to diffusion lengths comparable to system size: just as before, gradients (in this case in velocity ) are small, and the system behaves as a single unit. When Re is very large (flows with Re > 10,000 or even > 1,000,000 are common in the real world, though fortunately not in CVD reactors) diffusion of momentum only proceeds locally within very tiny cells, and huge gradients are possible: i.e. recirculating and turbulent flows. Note that, because the momentum that’s being carried is also doing the carrying, the equations are intrinsically nonlinear, and super-complicated stuff like turbulence can occur even in simple problems.

Too Hard for Simple Folk



In CVD we generally don’t even want to think about recirculation or turbulence, at least in the process chamber: it’s rather unlikely a turbulent reactor will give a reproducible and controllable result! So we will limit almost all of our analysis to some very simple cases:
  • plug flow, in which the fluid has only one velocity;
  • boundary-layer flow, in which a slow-moving part near walls and other objects meets plug flow in the middle;
  • fully developed flow, where the boundary layers have merged together.

These flows are the topics of the next few pages of the tutorial.






Return to Tutorial Table of Contents
Book version of the CVD Tutorial